The Dangers of One-Dimensional Over-Interaction Between Body and Soul

On By st4blogIn Uncategorized

With a 24 hours long break behind us, we assembled in the afternoon of day 8 for second in the series of lectures on SYK model by Pranjal (TIFR). He started with reviewing some results from the 1st day, including the value of b which was our homework problem.

Followed by this, he discussed an SYK-like (tensor) model.

\mathcal{L} = i\psi_j^{abc}\partial_t \psi _j^{abc} + i^{3/2}\frac{j}{3!}\psi_1\psi_2\psi_3\psi_4

where

\psi_1\psi_2\psi_3\psi_4 = \psi_1^{l_{14}l_{13}l_{12}}\psi_2^{l_{12}l_{24}l_{23}}\psi_3^{l_{23}l_{13}l_{34}}\psi_4^{l_{34}l_{24}l_{14}}

and l_{ij} is trifundamental representation of product of three copies of O(N). He made the remark that tensor models are unitary, though Hilbert space in these grows much faster than in SYK model because of large number of fermionic degrees of freedom. Most importantly, large N physics of tensor models is same as that of SYK model.

Next, we moved on to the large-q limit of the SYK model, when there’s a large number of fermions interacting at a time. It is in this limit that the model has been shown to be solvable. Pranjal proposed an ansatz in large q limit for the two-point function

G(\tau_1,\tau_2) = \frac{1}{2}sgn(\tau_1-\tau_2)\left\{1 + \frac{g(\tau)}{q} + \mathcal{O}(\frac{1}{q^2})\right\}

Here, first term is the two-point function in UV limit \& g(\tau) is an unknown function. Fourier transforming this equation and substituting it in Schwinger-Dyson equation gave the Fourier transformed expression for 1PI, \Sigma(\tau_1,\tau_2), which had been derived in the last lecture. Inverse transforming this \& solving the resulting differential equation

\frac{\partial_{\tau}^2}{q}\left\{sgn(\tau)g(\tau)\right\} = J^2 sgn(\tau)2^{1-q}e^{g(\tau)}

with boundary conditions g(0)=g(\beta)=0 gave the expression for g(\tau). Using this, one can write the two point function. During this, we had a cameo by Rohan Poojary (TIFR) who termed his explanation for sgn function on circle ‘the vaguest ever’! Though we were quite satisfied with it.

After this, we moved on to four-point functions, he termed them ‘ladder diagrams’.

WP_20170517_12_22_27_Pro

This equation is

\mathcal{F}_{n+1} = K * \mathcal{F}_n,

where n represents number of rungs in the ladder.

\mathcal{F} = \mathcal{F}_0 + K*K*\mathcal{F}_0 + ... = \frac{1}{1-K}*\mathcal{F}_0.

The above equation he wrote in the eigenbasis as,

\Sigma\frac{1}{1-K(n)}\frac{\langle\psi_n|\mathcal{F}_0\rangle}{\langle\psi_n|\psi_n\rangle}|\psi_n\rangle = \mathcal{F},

and started the program to evaluate its eigenvalues and eigenvectors.

He argued that K acting on the three-point function gives back the same three-point function in IR limit (J \rightarrow \infty).

 

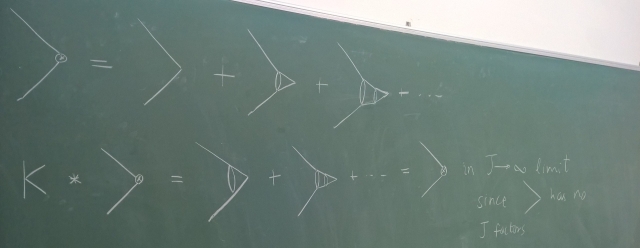WP_20170517_12_30_41_ProMotivated by this, he wrote the eigenvalue of K using the form of three-point function in a CFT. To find the eigenvectors of the kernel, he showed that it commutes with Casimir for conformal group implying that these may have simultaneous eigenvectors. By another argument, which he could not exactly formulate, it can be shown that kernel can be written as a function of Casimir. Thus one can find instead the eigenvectors of Casimir.

This is where he ended his lecture.

Madhusudhan Raman (IMSc) delivered the evening talk about basics of supersymmetry, in order to lay the groundwork for Victor’s talks on supersymmetric localization. He started with the Coleman-Mandula theorem which states that Poincare and internal symmetries cannot be combined an any way except trivially. Two interesting points came up during the discussion: (i) that this was a statement that was true under the assumption that the resulting theory has a non-trivial and analytic S-matrix, and (ii) that it doesn’t apply to lower-dimensional quantum field theories! Coleman and Mandula assumed that the group G is a Lie group. The way out is to Z_{2}-grade the algebra to include both commutators and anticommutators i.e.

[O_{a},O_{b}]=O_{a}O_{b}-(1)^{n_{a}n_{b}}O_{b}O_{a}

where,

n_{a} = 0 \text{ for bosonic operators and} \ 1 \text{ for fermionic operators.}

and he begin with definition of the supersymmetry algebra

(a)~~~~~ [Q_{\alpha},M^{\mu\nu}]= \iota (\sigma^{\mu\nu})_{\alpha}^{\beta}Q_{\beta}

where, Q_{\alpha} is a spin-1/2 operator so it transforms like

Q_{\alpha} \simeq(I-\iota \omega_{\mu\nu}\sigma)_\alpha^\beta Q_{\beta}.

Then, he spoke about the effect of translations,

(b)~~~~~~~~~~[Q_{\alpha},P^{\nu}]= 0.

He explained by logical argument that the above commutator can be fixed in a simple way: let’s assume it transformed as

[Q_{\alpha},P^{\mu}]= c(\sigma^{\mu})_{\alpha\dot{\alpha}}\bar{Q}^{\dot{\alpha}},

then since the l.h.s. satisfies Jacobi’s identity with respect to P^{\mu} i.e.

[P_{\mu},[P^{\mu},Q_{\beta}]]+cycl.= 0 ~ \text{which implies} \ c=0

Next came the effects of the supercharges on each other,

(c)~~~~~~\{Q_{\alpha},Q^{\beta}\}= K(\sigma^{\mu\nu})_{\alpha}^{\beta}M_{\mu\nu}

using the same arguments we can show K=0.

(d)~~~ \{Q_{\alpha},\bar{Q}_{\dot{\beta}}\}= 2(\sigma^{\mu})_{\alpha \dot{\beta}}P_{\mu}

From the last relation it is clear that the supersymmetry transformation knows about the underlying space-time and also he explained why supersymmetry commutes with internal symmetries which are clear from this relation,

[T_{a},Q_{\alpha}]=0.

Then he explained the R-symmetry

Q_{\alpha}\longrightarrow \exp{(\iota\gamma)}Q_{\alpha}\\ ,~~~~~Q_{\dot{\alpha}}\longrightarrow \exp{(-\iota\gamma)}Q_{\dot{\alpha}},~~~ \text{such that}~~ R:\exp{(-\iota\gamma t)}Q_{\alpha}\exp{(\iota\gamma t)}

It satisfies following relation

[Q_{a},R] = Q_{a} and

[\bar{Q}_{\dot{a}},R] =-\bar{Q}_{\dot{a}}

so we observe that the supercharges are charged under R-symmetry. Then, he extend the SUSY algebra for N charges

\{Q^{A}_{\alpha},\bar{Q}_{\dot{\beta},B}\}= 2(\sigma^{\mu})_{\alpha \dot{\beta}}P_{\mu}\delta^{A}_{B}

where, A,B = 1, 2, 3, …, N.

\{Q^{A}_{\alpha},Q_{\beta}^{B}\}= (\sigma^{\mu})_{\alpha \beta} Z_{A B},

where Z_{AB} is known as the central charge.

We know that Casmirs for Poincare algebra tell us how to label 1-particle states, i.e. we use the mass and spin/helicity.

C_{1}= P_{\mu}P^{\mu} and

C_{2}= W_{\mu}W^{\mu}; ~~~ W_{\mu}=1/2\epsilon_{\mu\nu\rho\sigma}P^{\nu}M^{\varrho\sigma}

then he explain what’s happen if we add SUSY (for example N=1) C_{1} is still a Casimir but C_{2} changes to a superspin that is defined by

C_{2}= C_{\mu\nu}C^{\mu\nu}; ~~~ C_{\mu\nu}=B_{\mu}P_{\nu}-B_{\nu}P_{\mu} \& ~~ B_{\mu}=W_{\mu}-\frac{1}{4}\bar{Q}_{\dot{\alpha}}\bar{\sigma}_{\mu}^{\dot{\alpha}\alpha}Q_{\dot{\alpha}}

Then he gave an example for N=1 supersymmetry for massless particles, where we boost to the frame P_{\mu}=(E,0,0,E). The SUSY algebra then gives

\{Q_{\alpha},\bar{Q}_{\dot{\beta}}\}= 4 E\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}

and we can define raising operator and lowering operators as

a=\frac{ Q_{1}}{2\sqrt{E}},~~~a^{+}=\frac{ \bar{Q}_{1}}{2\sqrt{E}}

We know that for the massless particles helicity is good quantum number, as demonstrated by

J^{3}a|P_{\mu}\lambda\rangle=(\lambda-1/2)a |P_{\mu}\lambda\rangle

In the last hour he spend the time to explain us a superspace (X^{\mu},\theta^{\alpha},\bar{\theta}^{\dot{\alpha}}) (the fermionic directions are the soul to the bosonic directions’ body, as pictured above) and super-field

F(X^{\mu},\theta^{\alpha},\bar{\theta}^{\dot{\alpha}})=f(x)+\theta\psi(x)+\bar{\theta}\bar{\psi}(x)+\theta\theta m(x)+\bar{\theta}\bar{\theta} n(x)+{\theta}\sigma^{\mu}\bar{\theta}v_{\mu}+{\theta}{\theta}\bar{\theta}\bar{\lambda}(x)+\bar{\theta}\bar{\theta} \theta \rho(x)+{\theta}{\theta}\bar{\theta}\bar{\theta}\phi(x)

Madhu stated that the idea of susysymmetry in superspace is lot like momentum in spacetime: it generates translations. We can give this idea a differential-operator meaning; just like momentum generates translations in space, supercharges generate translations in superspace!

Q_{\alpha}=-\iota \frac{\partial}{\partial\theta^{\alpha}}-\sigma_{\alpha\bar{\dot{\beta}}}^{\mu}\bar{\theta}^{\bar{\dot{\beta}}}\partial_{\mu}

\bar{Q}_{\dot{\beta}}=-\iota \frac{\partial}{\partial\bar{\theta}^{\dot{\beta}}}-\sigma_{\alpha\bar{\dot{\beta}}}^{\mu}\theta^{\alpha}\partial_{\mu}

How do superfields transform under infinitesimal coordinate changes generated by supercharges? It is simply

\delta_{\epsilon,\bar{\epsilon}}F=(\iota\epsilon Q+\iota\bar{\epsilon}\bar{Q})F.

Eventually, one would like to write down actions in superspace. However, the general superfield has far too many fields, corresponding to a reducible representation of the SUSY algebra. In order to cut down the number of components, one needs to define derivative operators in superspace that anticommute with the supercharges. These can then be used to (a) effect constraints on superfields, that will reduce the number of fields, and (b) write down superactions in superspace. These differential operators look like

D_{\alpha}=\frac{\partial}{\partial\theta}+\iota\sigma_{\mu}\bar{\theta}\partial_{\mu}

\bar{D}_{\alpha}=\frac{\partial}{\partial\bar{\theta}}+\iota\sigma_{\mu}\theta\partial_{\mu}

and

\{Q_{\alpha},D_{\alpha}\}=0

At the end, he explained that any action of the form

S=\int d^{2}\theta d^{2}\bar{\theta} f(x,\theta,\bar{\theta}) + \int d^{2}\theta w(x,\theta) + hc,

is — by construction! — SUSY invariant! The first term is known as the Kahler potential and the second is known as the superpotential. A short discussion of the statement of non-renormalization theorems followed, and that was where we concluded for the day.

Leave a comment